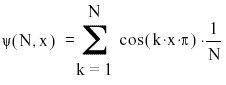
The wavefunction for a particle with an ill-defined location can be regarded as the sum (superposition) of several wavefunctions of different wavelength that interfere constructively in one place but destructively elsewhere. As more waves are used in the superposition, the location becomes more precise at the expense of uncertainty in the particle's momentum. An infinite number of waves is needed to construct the wavefunction of a perfectly localized particle. The wavefunction is given by
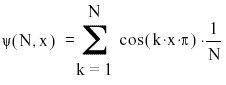
Where N is the number of waves to sum, x has units of m, and k has units of m-1. The constant 1 / N is introduced to keep the superpositions of the same overall magnitude.
To graph wavefunction enter the parameter (i.e., N) and hit New Plot. Up to 5 plots can be displayed at one time. The Clear button will remove all plots. To see the parameters for each plot hit the Legend on/off button. The Redraw button will refresh the graph. This is useful when the function domain (i.e., x ) has been changed. To see the value of each plot at a given point, move your cursor to the desired location then click and hold. Toggle between a plot of the wavefunction(s) and its square by clicking the checkbox.
A wavepacket moves and spreads with time. To see this effect we need to construct a superposition in which all components correspond to motion in the same direction. To do so we need a complex wavefunction:
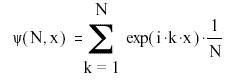
Moreover, we also need the time-dependent form:
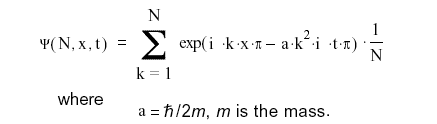
The real part of this wavefunction is:
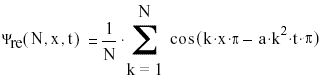
Where t has units of s, and a has units m2 s-1.
To show this equation over time click the Animation tab, then graph a wavefunction and hit the Start/Stop button. The Time step field may be used to change the time increment.
